Merge Sort

Merge Sort

Merge Sort is a comparison-based sorting algorithm that follows the Divide and Conquer strategy. It divides the unsorted array into two halves, sorts each half independently, and then merges the sorted halves to produce the final sorted array.

Here’s how the Merge Sort algorithm works:

1. Divide: Divide the unsorted array into two halves.
2. Conquer: Recursively sort the two halves.
3. Merge: Merge the two sorted halves to produce a single sorted array.

Here’s a high-level description of the Merge Sort algorithm:

• If the array has zero or one element, it is already sorted.
• If the array has more than one element, recursively divide the array into two halves.
• Recursively sort each half.
• Merge the sorted halves back together.

#include <stdio.h>
#include <stdlib.h>

// Merge two sorted subarrays arr[l..m] and arr[m+1..r]
void merge(int arr[], int l, int m, int r) {
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;

    // Create temporary arrays
    int L[n1], R[n2];

    // Copy data to temporary arrays L[] and R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    // Merge the temporary arrays back into arr[l..r]
    i = 0;
    j = 0;
    k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // Copy the remaining elements of L[], if any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    // Copy the remaining elements of R[], if any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// Merge Sort function
void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2; // Find the middle point
        // Recursively sort the first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
        // Merge the sorted halves
        merge(arr, l, m, r);
    }
}

// Print an array
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

// Driver program to test Merge Sort
int main() {
    int arr[] = {12, 11, 13, 5, 6, 7};
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("Original array: \n");
    printArray(arr, n);

    mergeSort(arr, 0, n - 1);

    printf("\nSorted array: \n");
    printArray(arr, n);
    return 0;
}

Output:

Original array: 
12 11 13 5 6 7 

Sorted array: 
5 6 7 11 12 13 

Code Explanation

1. merge Function

void merge(int arr[], int l, int m, int r) {
    int i, j, k;
    int n1 = m - l + 1; // Size of the left subarray
    int n2 = r - m;     // Size of the right subarray
 
    // Create temporary arrays
    int L[n1], R[n2];
 
    // Copy data to temporary arrays L[] and R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i]; // Copy left subarray
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j]; // Copy right subarray
 
    // Merge the temporary arrays back into arr[l..r]
    i = 0; // Initial index of the left subarray
    j = 0; // Initial index of the right subarray
    k = l; // Initial index of the merged subarray
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i]; // Place the smaller element in the merged array
            i++;
        } else {
            arr[k] = R[j]; // Place the smaller element in the merged array
            j++;
        }
        k++;
    }
 
    // Copy the remaining elements of L[], if any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    // Copy the remaining elements of R[], if any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

• Purpose: Merges two sorted subarrays (arr[l..m] and arr[m+1..r]) into a single sorted subarray.
• How it works:
  1. Calculates the sizes of the left (L) and right (R) subarrays.
  2. Copies the elements of the left and right subarrays into temporary arrays L and R.
  3. Merges the two subarrays back into the original array arr in sorted order:
     • Compares elements from L and R and places the smaller element in arr.
     • Copies any remaining elements from L or R into arr.

2. mergeSort Function

void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2; // Find the middle point
        // Recursively sort the first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
        // Merge the sorted halves
        merge(arr, l, m, r);
    }
}

• Purpose: Recursively sorts the array using the Merge Sort algorithm.
• How it works:
  1. Checks if the left index (l) is less than the right index (r). If not, the subarray is already sorted.
  2. Calculates the middle index (m) to divide the array into two halves.
  3. Recursively sorts the left half (arr[l..m]) and the right half (arr[m+1..r]).
  4. Merges the two sorted halves using the merge function.

3. printArray Function

void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        printf("%d ", arr[i]); // Print each element
    printf("\n"); // Move to the next line after printing
}

• Purpose: Prints the elements of the array.
• How it works:
  • Iterates through the array and prints each element followed by a space.
  • After printing all elements, it adds a newline (\n) for better readability.

4. main Function

int main() {
    int arr[] = {12, 11, 13, 5, 6, 7}; // Unsorted array
    int n = sizeof(arr) / sizeof(arr[0]); // Calculate array size
 
    printf("Original array: \n");
    printArray(arr, n); // Print original array
 
    mergeSort(arr, 0, n - 1); // Sort the array
 
    printf("\nSorted array: \n");
    printArray(arr, n); // Print sorted array
    return 0;
}

• Purpose: Drives the program.
• How it works:
  1. Declares and initializes an array arr with unsorted integers.
  2. Calculates the size of the array (n) using sizeof(arr) / sizeof(arr[0]).
  3. Prints the original array using the printArray function.
  4. Calls the mergeSort function to sort the array.
  5. Prints the sorted array using the printArray function.

Key Points

1. Merge Sort:
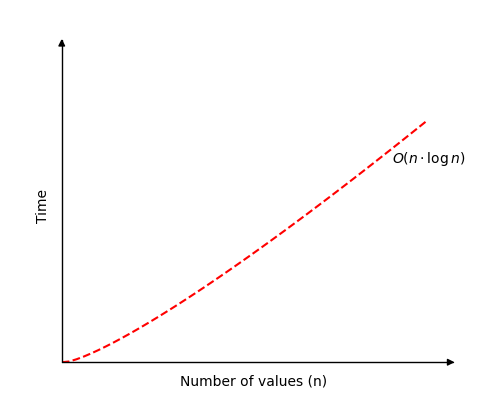
   • Time Complexity: O(n log n) in all cases (worst, average, and best).
   • Space Complexity: O(n) (requires additional space for temporary arrays).
   • It is a stable and efficient sorting algorithm for large datasets.
2. How Merge Sort Works:
   • Divides the array into two halves recursively until each subarray contains a single element.
   • Merges the sorted subarrays back together in sorted order.
3. Advantages:
   • Consistent performance (always O(n log n)).
   • Suitable for sorting linked lists and external sorting.