Index
Quick Sort
Quick Sort is a highly efficient sorting algorithm and is based on the principle of divide and conquer. It works by selecting a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays according to whether they are less than or greater than the pivot. The sub-arrays are then recursively sorted.
Algorithm
Here’s how the Quick Sort algorithm works:
- Choose a pivot: Select a pivot element from the array. There are various strategies for choosing a pivot element, such as selecting the first, last, middle, or a random element.
- Partitioning: Reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it. After this partitioning, the pivot is in its final sorted position.
- Recursively sort sub-arrays: Apply the Quick Sort algorithm recursively to the sub-arrays of elements with smaller values and separately to the sub-array of elements with greater values.
- Combine: The sub-arrays become sorted, and when all the recursive calls finish, the entire array is sorted.
Here’s a simple implementation of the Quick Sort algorithm in c:
#include <stdio.h>
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // Pivot (last element)
int i = (low - 1); // Index of smaller element
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than or equal to pivot
if (arr[j] <= pivot) {
i++; // Increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
// pi is partitioning index, arr[pi] is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {11, 71, 1, 56, 34, 5};
int n = sizeof(arr) / sizeof(arr[0]);
printf("Original array: \n");
printArray(arr, n);
quickSort(arr, 0, n - 1);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
Output:
Original array:
11 71 1 56 34 5
Sorted array:
1 5 11 34 56 71
Code Explanation
1. swap Function
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}- Purpose: Swaps two integers.
- How it works:
- Takes two pointers (
aandb) as arguments. - Uses a temporary variable (
t) to swap the values pointed to byaandb.
- Takes two pointers (
2. partition Function
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // Pivot (last element)
int i = (low - 1); // Index of smaller element
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than or equal to pivot
if (arr[j] <= pivot) {
i++; // Increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}- Purpose: Partitions the array into two subarrays around a pivot element.
- How it works:
- Selects the last element (
arr[high]) as the pivot. - Initializes
ias the index of the smaller element (low - 1). - Iterates through the array from
lowtohigh - 1:- If the current element (
arr[j]) is less than or equal to the pivot, it incrementsiand swapsarr[i]andarr[j].
- If the current element (
- After the loop, swaps the pivot (
arr[high]) witharr[i + 1]to place the pivot in its correct position. - Returns the index of the pivot (
i + 1).
- Selects the last element (
3. quickSort Function
void quickSort(int arr[], int low, int high) {
if (low < high) {
// pi is partitioning index, arr[pi] is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}- Purpose: Recursively sorts the array using the Quick Sort algorithm.
- How it works:
- Checks if
lowis less thanhigh(i.e., there are at least two elements to sort). - Calls the
partitionfunction to partition the array and get the pivot index (pi). - Recursively sorts the subarrays before and after the pivot:
quickSort(arr, low, pi - 1)sorts the left subarray.quickSort(arr, pi + 1, high)sorts the right subarray.
- Checks if
4. printArray Function
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]); // Print each element
printf("\n"); // Move to the next line after printing
}- Purpose: Prints the elements of the array.
- How it works:
- Iterates through the array and prints each element followed by a space.
- After printing all elements, it adds a newline (
\n) for better readability.
5. main Function
int main() {
int arr[] = {11, 71, 1, 56, 34, 5}; // Unsorted array
int n = sizeof(arr) / sizeof(arr[0]); // Calculate array size
printf("Original array: \n");
printArray(arr, n); // Print original array
quickSort(arr, 0, n - 1); // Sort the array
printf("Sorted array: \n");
printArray(arr, n); // Print sorted array
return 0;
}- Purpose: Drives the program.
- How it works:
- Declares and initializes an array
arrwith unsorted integers. - Calculates the size of the array (
n) usingsizeof(arr) / sizeof(arr[0]). - Prints the original array using the
printArrayfunction. - Calls the
quickSortfunction to sort the array. - Prints the sorted array using the
printArrayfunction.
- Declares and initializes an array
Key Points
- Quick Sort:
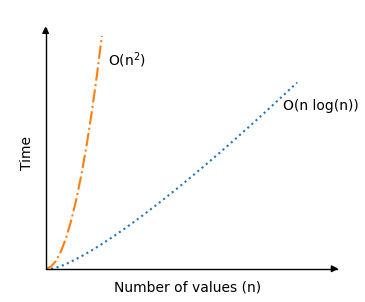
- Time Complexity: O(n log n) on average, but O(n²) in the worst case (e.g., when the array is already sorted).
- Space Complexity: O(log n) due to recursive calls.
- It is a highly efficient sorting algorithm for large datasets.
- How Quick Sort Works:
- Divides the array into two subarrays using a pivot element.
- Recursively sorts the subarrays.
- Partitioning:
- The
partitionfunction ensures that all elements smaller than the pivot are on the left, and all elements greater than the pivot are on the right .
- The