Selection Sort

Selection Sort

Selection Sort is a simple sorting algorithm that divides the input array into two parts: the sorted part and the unsorted part. Initially, the sorted part is empty, and the unsorted part contains all the elements of the array. The algorithm repeatedly selects the smallest (or largest) element from the unsorted part and moves it to the beginning (or end) of the sorted part. This process continues until the entire array is sorted.

Here’s how the Selection Sort algorithm works:

Algorithm:

1. Divide the input array into two parts: the sorted part and the unsorted part.
2. Find the smallest element in the unsorted part.
3. Swap the smallest element with the first element of the unsorted part, effectively adding it to the sorted part.
4. Repeat steps 2 and 3 for the remaining unsorted part of the array until the entire array is sorted.

#include <stdio.h>

// Function to perform Selection Sort
void selectionSort(int arr[], int n) {
    int i, j, min_index;

    // Traverse through all array elements
    for (i = 0; i < n - 1; i++) {
        // Find the minimum element in the unsorted part
        min_index = i;
        for (j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }

        // Swap the found minimum element with the first element
        int temp = arr[i];
        arr[i] = arr[min_index];
        arr[min_index] = temp;
    }
}

// Function to print an array
void printArray(int arr[], int size) {
    int i;
    for (i = 0; i < size; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

// Driver program to test above functions
int main() {
    int arr[] = {64, 25, 12, 22, 11};
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("Original array: \n");
    printArray(arr, n);
    selectionSort(arr, n);
    printf("Sorted array: \n");
    printArray(arr, n);
    return 0;
}

Output:

Original array: 
64 25 12 22 11 
Sorted array: 
11 12 22 25 64 

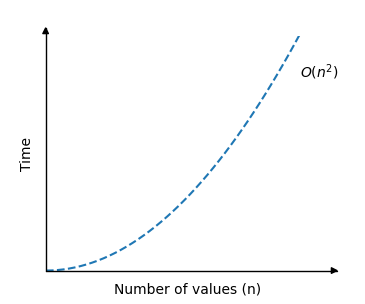
Selection Sort Time Complexity

The time complexity of the Selection Sort algorithm is O(n^2) in all cases, where n is the number of elements in the array.

Here’s why the time complexity is O(n^2):

• Selection Sort works by repeatedly finding the minimum (or maximum) element from the unsorted part of the array and moving it to the beginning (or end) of the sorted part.
• In the worst-case scenario, Selection Sort performs a maximum number of comparisons and swaps to sort the array.
• For each element in the array, Selection Sort scans the remaining unsorted part of the array to find the minimum (or maximum) element.
• The number of comparisons and swaps required to sort the array is proportional to n^2.
• As a result, the time complexity of Selection Sort is O(n^2) in all cases.